误差理论

Gaußfehlerkurven für zwei Standardabweichungen

误差理论（误差分析）用来估计测量结果的准确性。

随机误差是指在完全相同条件下产生了不同的测量结果。一般情况下，通过计算算术平均值可以相互抵消这些测量误差。

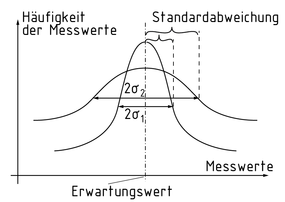
对于大量的测量结果，可以通过高斯误差曲线，也称“钟形”曲线、正态分布，对测量结果的频率进行描述。正态分布的参数为期望 $\bar{I}$ 和标准差 $\sigma $。

若进行多次重复测量时，测量结果忽高忽低，往往说明存在系统误差。测量过程中所产生的系统误差可以利用数学期望进行观测。

系统误差主要由读取结果错误造成，包括环境影响，错误操作等。

两个标准差的高斯误差曲线

近义词

随机误差

系统误差

Fehlerrechnung

Gaußfehlerkurven für zwei Standardabweichungen

Die Fehlerrechnung dient zur Abschätzung der Genauigkeit eines Messergebnisses.

Liefert eine mehrfach durchgeführte Messung unter exakt gleichen Bedingungen gestreute Ergebnisse, liegen zufällige Fehler vor. Im Mittel heben sich diese Messfehler auf, sodass durch die Berechnung des arithmetischen Mittels auf das Resultat geschlossen werden kann.

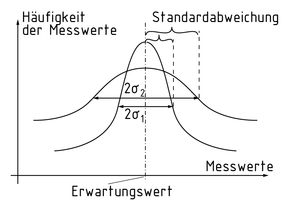
Liegen genügend Messwerte vor, können sie als Häufigkeitsverteilung in der Gaußschen Fehlerkurve dargestellt werden. Die Gaußsche Fehlerkurve wird auch als Glockenkurve oder Normalverteilung bezeichnet. Parameter der Normalverteilung sind der Erwartungswert $\bar{I}$ und die Standardabweichung $\sigma $.

Ein systematischer Fehler liegt vor, wenn sich aus mehreren Messungen zu hohe bzw. zu niedrige Ergebnisse ergeben. Für die Messung gilt dann ein sogenannter Erwartungswert, der den systematischen Fehler berücksichtigt.

Die Ursachen für systematische Fehler können u. a. beim Ablesen der Messwerte, durch Umwelteinflüsse oder ungenaue Justierung entstehen.

Theory of errors

Gaussian error curves for two standard deviations

The theory of errors (error analysis) is used to estimate the accuracy of a measuring result.

If a measurement performed several times under identical conditions produces scattered results, random errors exist. These measuring errors cancel each other out in the average, which means that the result can be deduced by calculating the arithmetic mean.

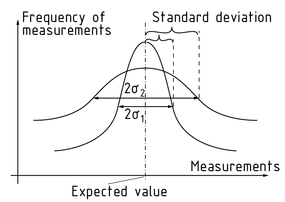
If a sufficient number of measurements are available, they can be depicted in the form of a frequency Scale in a Gaussian error curve, also called a bell curve or normal distribution curve. Normal distribution parameters are the expected value $\bar{I}$ and the Standard deviation $\sigma $.

A systematic error exists if several measurements produce results that are too high or too low. An expected value that takes the systematic error into account then applies to the measurement.

Causes of systematic errors when reading off measured values include environmental influences and inaccurate adjustment.

Teoría de los errores

Curvas de error de Gauss para dos desviaciones estándar

La teoría de los errores (análisis del error) se usa para estimar la precisión de un resultado de medición.

Si una medición realizada varias veces bajo condiciones idénticas produce resultados dispersos, existen errores aleatorios. Estos errores de medición se cancelan entre sí en el promedio, lo que significa que el resultado puede ser deducido calculando la media aritmética.

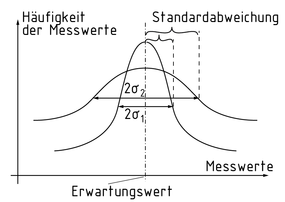
Si hay disponible un número suficiente de mediciones, estas se pueden mostrar en la forma de una escala de frecuencia en una curva de error de Gauss, también llamada curva de campana o curva de distribución normal. Los parámetros de distribución normal son el valor esperado $\bar{I}$ y la desviación estándar $\sigma $ .

Existe un error sistemático si varias mediciones producen resultados que son demasiado altos o demasiado bajos. Un valor esperado considera el error sistemático y luego aplica a la medición.

Las causas de los errores sistemáticos cuando se leen valores medidos incluyen influencias ambientales y ajustes imprecisos.

Curvas de error de Gauss para dos desviaciones estándar