
一种定义
四种语言
0,1,2
- 德國
- 英語
- 中國
- 西班牙語
动量矩
角动量L是一个守恒的物理量,它作用于旋转体上,方向与转轴旋转方向一致。动量矢量 $\overrightarrow{L}$ 的方向可由物体旋转方向判断,然而对应力矩的矢量 $\overrightarrow{M}$ 方向需由右手法则(右手螺旋)判定。
角动量矢量 $\overrightarrow{L}$ 是位置向量 $\vec{r}$ 与该点和路径相切的动量共同作用的结果 $\overrightarrow{p}$ 。
旋转物体的角动量
角动量L可由质量惯性矩J和角速度$\omega $计算得到,公式如下:$L=J\cdot \omega $
角动量随时间$\Delta t$的变化情况 $\Delta \overrightarrow{L}$ 取决于如下不断变化的角动量矢量 $\overrightarrow{M}$ :$\Delta \overrightarrow{L}=\overrightarrow{M}\cdot \Delta t$
角动量守恒定律(也称作角动量定理)是指在独立的物理系统中角动量守恒。一旦物体开始转动,在不受外力矩作用时物体将无限转动下去。
Impulsmoment
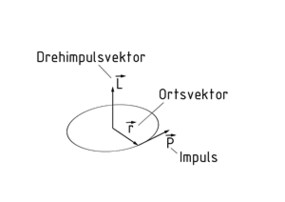
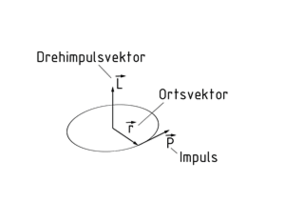
Der Drehimpuls L ist eine physikalische Erhaltungsgröße, die auf einen rotierenden Körper und mit der gleichen Orientierung wie dessen Drehachse wirkt. In Abhängigkeit der Drehrichtung und somit des Drehmomentvektors$\overrightarrow{M}$ lässt sich mit der Regel der rechten Hand (Rechtsschraube) die Richtung des Drehimpulsvektors $\overrightarrow{L}$ ermitteln.
Das Kreuzprodukt des Ortsvektors \[\vec{r}\] und dem in diesem Punkt tangential zur Bahn herrschenden Impuls $\overrightarrow{p}$ liefert den Vektor des Drehimpulses $\overrightarrow{L}$.
Der Betrag des Drehimpulses L setzt sich aus dem Massenträgheitsmoment J und der Winkelgeschwindigkeit $\omega $ zusammen. Es gilt: $L=J\cdot \omega $
In Abhängigkeit des wirkenden Drehmomentvektors $\overrightarrow{M}$ ist die Drehimpulsänderung $\Delta \overrightarrow{L}$ über die Zeitdifferenz $\Delta t$ wie folgt zu ermitteln: \[\Delta \overrightarrow{L}=\overrightarrow{M}\cdot \Delta t\]
Der Drehimpulserhaltungssatz (auch Drallsatz) beschreibt die Erhaltung des Drehimpulses in einem isolierten physikalischen System. Ein einmal in Rotation versetzter Körper führt somit die Drehbewegung unendlich fort, solange kein weiteres Moment auf ihn wirkt.
Moment of momentum
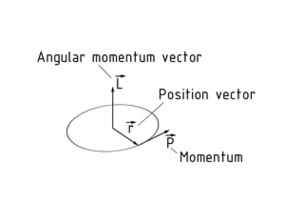
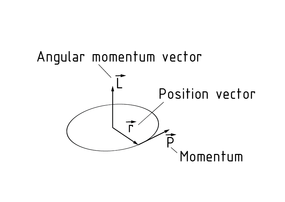
The angular momentum L is a conserved physical quantity that acts on a rotating body in the same direction as its axis of Rotation. The direction of the angular momentum vector $\overrightarrow{L}$ can be determined based on the direction of rotation and thus the torque vector$\overrightarrow{M}$ using the right-hand rule (right-hand helix).
The Vector of the angular momentum $\overrightarrow{L}$is the cross product of the position vector \[\vec{r}\] and the momentum tangential to the path at this point $\overrightarrow{p}$.
The angular momentum L is calculated from the mass moment of inertia J and the angular Velocity $\omega $ as follows: $L=J\cdot \omega $
The change in angular momentum $\Delta \overrightarrow{L}$ over the time difference $\Delta t$ is determined based on the active angular momentum vector $\overrightarrow{M}$ as follows: \[\Delta \overrightarrow{L}=\overrightarrow{M}\cdot \Delta t\]
The angular Momentum conservation law (also called the principle of angular momentum) refers to the conservation of angular momentum in an isolated physical system. Once rotation has been initiated in a body, it continues indefinitely as long as no other moment acts on the body.
Momento de impulso
El momento angular L es una cantidad física conservada que actúa en un cuerpo en rotación en la misma dirección que su eje de rotación. La dirección del vector de momento angular $\overrightarrow{L}$ puede ser determinada basada en la dirección de rotación y, por lo tanto, el vector de torque $\overrightarrow{M}$ puede ser determinado usando la regla de mano derecha (hélice derecha).
El vector del momento angular $\overrightarrow{L}$ es el producto cruzado del vector de posición $\vec{r} $ y el momento tangencial a la ruta en este punto $\overrightarrow{p}$ .
Momento angular de un cuerpo en rotación.
El momento angular L se calcula a partir del momento de inercia de la masa J y la velocidad angular $\omega $ según lo siguiente: $L=J\cdot \omega $
El cambio en el momento angular $\Delta \overrightarrow{L}$ sobre la diferencia de tiempo $\Delta t$ es determinado basado en el vector del momento angular activo $\overrightarrow{M}$ según lo siguiente: $\Delta \overrightarrow{L}=\overrightarrow{M}\cdot \Delta t $
La ley de conservación del impulso angular (también llamada principio de momento angular) se refiere a la conservación del momento angular en un sistema físico aislado. Una vez que se ha iniciado la rotación en un cuerpo, esta continúa indefinidamente mientras que ningún otro momento actúe sobre el cuerpo.
