
Wählen Sie eine
oder mehrere Sprachen aus
0,1,0
- Deutsch
- Englisch
- Chinesisch
- Spanisch
Mohrscher Spannungskreis
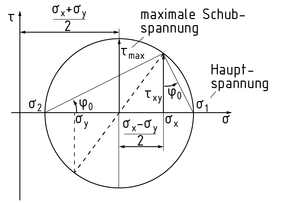
Der Mohrsche Spannungskreis ermöglicht die geometrische Transformation von Spannungen zu den Koordinatenachsen (${{\sigma }_{x}},~{{\sigma }_{y}}$ und$~{{\tau }_{xy}}$) in die herrschenden Spannungen einer Scheibe (${{\sigma }_{\xi }},~{{\sigma }_{\eta }}$ und ${{\tau }_{\xi \eta }}$) und unter einem beliebigen Winkel ${{\varphi }_{0}}$. Ein Kreis mit dem Radius r wird in einem $\tau -\sigma $-Diagramm gezeichnet. Für die Konstruktion des Mohrschen Spannungskreises müssen${{\sigma }_{x}},{{\sigma }_{y}}$ und ${{\tau }_{xy}}$ bekannt sein.
Folgende Schritte zur Konstruktion des Spannungskreises sind notwendig:
- ${{\sigma }_{x}}$ und ${{\sigma }_{y}}$ auf der $\sigma $-Achse einzeichnen.
- Den Mittelpunkt des Kreises bei \[\frac{({{\sigma }_{x}}+{{\sigma }_{y}})}{2}\] bestimmen.
- Die Schubspannung ${{\tau }_{xy}}$ bei ${{\sigma }_{x}}$ eintragen.
- Einen Kreis um den Mittelpunkt durch den Punkt $({{\sigma }_{x}},{{\tau }_{xy}})$ schlagen. Der Kreisradius r entspricht dem Betrag der maximalen Schubspannung ${{\tau }_{\max }}$.
- Die erste Hauptspannung ${{\sigma }_{1}}$ ermitteln, die dem rechten Schnittpunkt des Kreises mit der $\sigma $-Achse entspricht.
- Die zweite Hauptspannung${{\sigma }_{2}}$ermitteln, die dem linken Schnittpunkt des Kreises mit der $\sigma $-Achse entspricht.
Mohr's circle
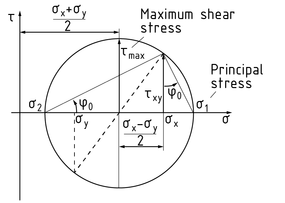
Mohr's circle is used to geometrically transform the stresses at the coordinate axes (${{\sigma }_{x}},~{{\sigma }_{y}}$ and$~{{\tau }_{xy}}$) into the prevailing stresses (${{\sigma }_{\xi }},~{{\sigma }_{\eta }}$ and ${{\tau }_{\xi \eta }}$) acting on a slice at any desired angle ${{\varphi }_{0}}$. A circle with the radius r is drawn in a $\tau -\sigma $ diagram. ${{\sigma }_{x}},{{\sigma }_{y}}$ and ${{\tau }_{xy}}$ must be known to create the Mohr's circle.
The relevant steps are as follows:
- ${{\sigma }_{x}}$ Plot and ${{\sigma }_{y}}$ on the $\sigma $-axis.
- Determine the centre of the circle based on \[\frac{({{\sigma }_{x}}+{{\sigma }_{y}})}{2}\].
- Enter the shear stress ${{\tau }_{xy}}$ at ${{\sigma }_{x}}$.
- Draw a circle around the centre point and through the point $({{\sigma }_{x}},{{\tau }_{xy}})$. The circle's radius r is equivalent to the maximum shear stress ${{\tau }_{\max }}$.
- Determine the first principal stress ${{\sigma }_{1}}$, which corresponds to the circle's point of intersection with the $\sigma $-axis on the right-hand side.
- Determine the second principal stress${{\sigma }_{2}}$, which corresponds to the circle's point of intersection with the $\sigma $-axis on the left-hand side.
莫尔应力圆
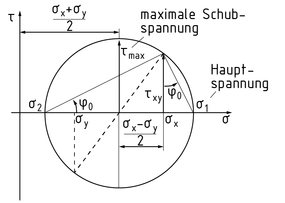
莫尔应力圆是用于将坐标系上的应力分量( ${{\sigma }_{x}},~{{\sigma }_{y}}$ 和 $~{{\tau }_{xy}}$ ) 转变为适用于任一给定角度 ${{\varphi }_{0}}$ 的平面单元上的应力分量 ( ${{\sigma }_{\xi }},~{{\sigma }_{\eta }}$ 和 ${{\tau }_{\xi \eta }}$ )。做一个半径为r的圆于 $\tau -\sigma $ 中。必须知道 ${{\sigma }_{x}},{{\sigma }_{y}}$ 和 ${{\tau }_{xy}}$ 才能创建一个莫尔应力圆。
相关步骤如下:
在坐标轴 $\sigma $ 轴上标出 ${{\sigma }_{x}}$ 和 ${{\sigma }_{y}}$ 。
根据 $\frac{({{\sigma }_{x}}+{{\sigma }_{y}})}{2}$ 确定圆心。
在 ${{\sigma }_{x}}$ 上做出剪应力 ${{\tau }_{xy}}$ 。
以圆心做圆并经过点 ( ${{\sigma }_{x}},{{\tau }_{xy}}$ )。圆的半径r等于最大剪应力 ${{\tau }_{\max }}$ 的值。
确定第一主应力 ${{\sigma }_{1}}$ ,其值等于莫尔圆与 $\sigma $ -轴在右手侧的交点。
确定第二主应力 ${{\sigma }_{2}}$ ,其值等于莫尔圆与 $\sigma $ -轴在左手侧的交点。
莫尔应力圆
Círculo de Mohr
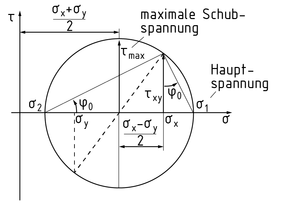
El círculo de Mohr se usa para transformar geométricamente los esfuerzos en los ejes de coordenadas ( ${{\sigma }_{x}},~{{\sigma }_{y}}$ y${{\tau }_{xy}}$ ) en los esfuerzos prevalecientes ( ${{\sigma }_{\xi }},~{{\sigma }_{\eta }}$ y ${{\tau }_{\xi \eta }}$ ) que actúan en una rebanada en cualquier ángulo deseado ${{\varphi }_{0}}$ . Se dibuja un círculo con un radio r en un $\tau -\sigma $ diagrama. ${{\sigma }_{x}},{{\sigma }_{y}}$ y ${{\tau }_{xy}}$ deben ser conocidas para crear el círculo de Mohr.
Los pasos relevantes son los siguientes:
${{\sigma }_{x}}$ Trazar y ${{\sigma }_{y}}$ en el eje $\sigma $ .
Determinar el centro del círculo basado en $\frac{({{\sigma }_{x}}+{{\sigma }_{y}})}{2}$ .
Ingresar el esfuerzo de corte ${{\tau }_{xy}}$ en ${{\sigma }_{x}}$ .
Dibujar un círculo alrededor del punto central y a través del punto $({{\sigma }_{x}},{{\tau }_{xy}})$ . El radio r del círculo es equivalente al esfuerzo de corte máximo ${{\tau }_{\max }}$ .
Determinar el primer esfuerzo principal ${{\sigma }_{1}}$ , el cual corresponde al punto de intersección del círculo con el eje $\sigma $ en el lado derecho.
Determinar el segundo esfuerzo principal ${{\sigma }_{2}}$ , el cual corresponde al punto de intersección del círculo con el eje $\sigma $ en el lado izquierdo.
Círculo de Mohr
