Normalspannung

Normalkraft auf einem Balken

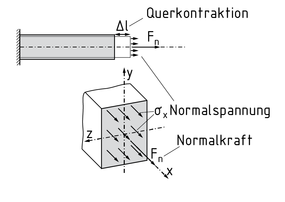
Eine Normalspannung $\sigma $ ist eine durch eine Normalkraft ${{F}_{N}}$ausgelöste Spannung auf eine Fläche A. In Körpern werden Normalkräfte durch Zug und Druck erzeugt. Es werden drei Normalspannungen unterschieden: ${{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}}$. Ihr Index gibt an, in welche Richtung sie wirken.

Sie berechnet sich wie folgt: $\sigma =\frac{{{F}_{N}}}{A}$

Die Normalspannung ist immer senkrecht zur Schnittebene. Eine Zugkraft ${{F}_{N}}$ auf ein Balkenelement hat die gleiche Orientierung wie die Balkenachse. Die Folge einer auf einem Balken wirkenden Zugkraft ${{F}_{N}}$ (mit symmetrischem Profil) ist die Verlängerung des Balkens, während er sich verschmälert. Das Verschmälern wird als Querkontraktion bezeichnet, die von der Querkontraktionszahl v abhängig ist. Eine wirkende Druckkraft löst eine Verkürzung (Stauchung) des Balkenelements und somit eine Querschnittsvergrößerung aus.

Normal stress

Normal force on a beam

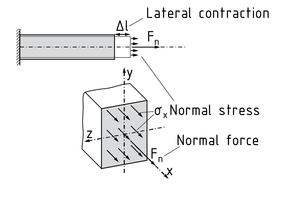
A normal stress $\sigma $ is a stress on an area A induced by a normal Force ${{F}_{N}}$. Tension and compression generate normal forces in bodies. There are three different normal stresses: ${{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}}$. The index indicates the direction in which they act.

They are calculated as follows: $\sigma =\frac{{{F}_{N}}}{A}$

The normal stress is always perpendicular to the sectional plane. A tensile force ${{F}_{N}}$ on a beam element acts in the same direction as the beam axis. A tensile force ${{F}_{N}}$ (with a symmetrical profile) acting on a beam makes it longer and narrower. This narrowing is referred to as lateral contraction, which is based on the Poisson ratio v. A compressive force acting on the beam element shortens (compresses) it, which increases the cross-section.

正应力

作用于梁上的法向力

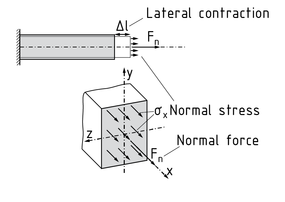
正应力 $\sigma $ 是由于截面A受到垂直于截面的 法向力 ${{F}_{N}}$ 而产生的。物体受到拉伸和压缩会生成法向力。总共产生 3 个不同的正应力： ${{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}}$ 。角标表明受力方向。

其计算方式如下： $\sigma =\frac{{{F}_{N}}}{A}$

正应力总是垂直于截面平面。 作用于梁单元上的拉伸力 ${{F}_{N}}$ 与梁轴线平行。拉伸力 ${{F}_{N}}$ （具有对称性）使梁具有伸长和变窄的趋向。这种变窄的趋向，我们称之为横向收缩，根据泊松比 v 计算横向收缩比。作用于梁单元上的压缩力使梁具有缩短（压缩）的趋向，使其横截面具有增大的趋向。

作用于梁上的法向力

Esfuerzo normal

Fuerza normal en una viga

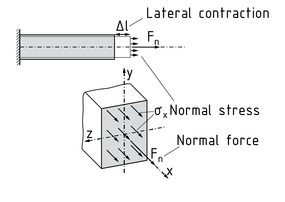
Un esfuerzo normal $\sigma $ es un esfuerzo en un área A inducido por una fuerza normal ${{F}_{N}}$ . La tensión y la compresión generan fuerzas normales en los cuerpos. Hay tres esfuerzos normales diferentes: ${{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}}$ . El índice indica la dirección en la cual actúan.

Se calculan de la siguiente manera: $\sigma =\frac{{{F}_{N}}}{A}$

El esfuerzo normal siempre es perpendicular al plano de sección. Una fuerza de tensión ${{F}_{N}}$ en un elemento de viga actúa en la misma dirección que el eje de la viga. La fuerza de tensión ${{F}_{N}}$ (con un perfil simétrico) que actúa en una viga la hace más larga o más corta. Este estrechamiento es referido como contracción lateral, la cual se basa en la relación de Poisson v. Una fuerza de compresión que actúa sobre un elemento de viga la acorta (comprime), lo que incrementa la sección.

Fuerza normal en una viga