Poissonzahl

Querkontraktion und Zugbeanspruchung

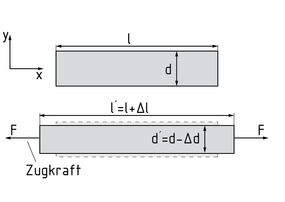
Die Poissonzahl $\upsilon $ ist eine dimensionslose Kenngröße der Querkontraktion eines Körpers unter Zugbeanspruchung. Sie wird auch als Querkontraktionszahl bezeichnet.

Wirkt eine Zugkraft (z. B. in x-Richtung) auf einen Körper, so dehnt er sich in diese Richtung. Darüber hinaus dehnt sich der Körper quer zur Zugrichtung (in y-Richtung) und verkleinert seinen Querschnitt. Dieses Verhalten der Dehnung quer zur Zugrichtung heißt Querkontraktion. Die Querkontraktionszahl bzw. Poissonzahl beschreibt das Verhältnis zwischen Längs- \[{{\varepsilon }_{x}}\] und Querdehnung \[{{\varepsilon }_{y}}\]und ist vom Material des Körpers abhängig. Es gilt: $\upsilon =-\frac{{{\varepsilon }_{y}}}{{{\varepsilon }_{x}}}$ mit ${{\varepsilon }_{y}}=\frac{\Delta d}{d}$ und ${{\varepsilon }_{x}}=\frac{\Delta l}{l}$.

Poisson number

Lateral contraction and tensile stress

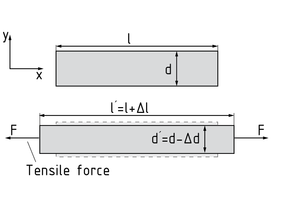
The Poisson number $\upsilon $ is a dimensionless parameter for a body's lateral contraction under tensile stress. It is also called the Poisson ratio.

If a tensile Force acts on a body (e.g. in the x-direction), it stretches in this direction. The body is also deformed perpendicular to the direction of the tension (in the y-direction) and its cross-section becomes smaller. This strain (deformation) perpendicular to the direction of the tension is called lateral contraction. The Poisson ratio / number indicates the ratio of longitudinal ${{\varepsilon }_{x}}$ to lateral strain ${{\varepsilon }_{y}}$ and depends on the Material from which the body is made. The following applies: $\upsilon =-\frac{{{\varepsilon }_{y}}}{{{\varepsilon }_{x}}}$ here ${{\varepsilon }_{y}}=\frac{\Delta d}{d}$ and ${{\varepsilon }_{x}}=\frac{\Delta l}{l}$.

泊松数

横向收缩和拉伸应力

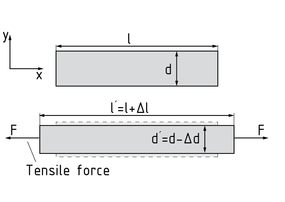
泊松数 $\upsilon $ 是无量纲量，反映了物体在拉伸应力作用下横向收缩的情况。又称为泊松比。

拉力作用于物体上时（如以 x 为方向），物体产生相同方向上的形变。物体还会产生垂直方向上的形变（在 y 轴方向），其横截面有变窄的趋势。垂直于拉力的应变 （形变）被称为横向收缩。泊松比 / 泊松数 是指纵轴方向的应变 ${{\varepsilon }_{x}}$ 与横向应变 ${{\varepsilon }_{y}}$ 的比值，取决于物体的材料特性。以下公式成立： $\upsilon =-\frac{{{\varepsilon }_{y}}}{{{\varepsilon }_{x}}}$ here ${{\varepsilon }_{y}}=\frac{\Delta d}{d}$ and ${{\varepsilon }_{x}}=\frac{\Delta l}{l}$ 。

横向收缩和拉伸应力

Número de Poisson

Contracción lateral y esfuerzo a tensión

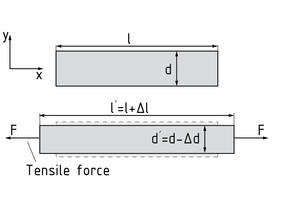
El número de Poisson $\upsilon $ es un parámetro sin dimensiones para la contracción lateral de un cuerpo bajo esfuerzo a tensión. También se llama la relación de Poisson.

Si una fuerza de tensión actúa en un cuerpo (por ejemplo, en la dirección x), este se estira en esta dirección. El cuerpo también se deforma perpendicularmente en la dirección de la tensión (en la dirección y) y su sección se vuelve más pequeña. Esta deformación perpendicular de la dirección de la tensión se llama contracción lateral. La relación/el número de Poisson indica la relación de la deformación longitudinal ${{\varepsilon }_{x}}$ y lateral ${{\varepsilon }_{y}}$ , y depende del material del que esté hecho el cuerpo. Aplica lo siguiente: $\upsilon =-\frac{{{\varepsilon }_{y}}}{{{\varepsilon }_{x}}} $ aquí ${{\varepsilon }_{y}}=\frac{\Delta d}{d} $ y ${{\varepsilon }_{x}}=\frac{\Delta l}{l} $ .

Contracción lateral y esfuerzo a tensión