Momentum conservation law

Impulserhaltung beim Stoßprozess zweier Kugeln

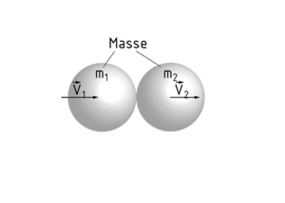
The momentum conservation law defines the consistency of total momentum in a closed system.

In an ideal impulse scenario, the momentum $\overrightarrow{p}$ before the impulse is equal to $\overrightarrow{p}'$ after the impulse. The interaction between two bodies as they collide with each other (with the relevant Velocity $\overrightarrow{v}$ and mass m) does not result in a loss of momentum.

The following applies: ${{m}_{1}}{{\overrightarrow{v}}_{1}}+{{m}_{2}}{{\overrightarrow{v}}_{2}}={{m}_{1}}\overrightarrow{v}{{'}_{1}}+{{m}_{2}}\overrightarrow{v}{{'}_{2}}$.

Interactions with the environment such as Friction effects are discounted, as the system in question is closed. This is a theoretical method of approach, but it does make complex systems calculable.

In practice, it is not possible to create a completely closed system.

Impulssatz

Impulserhaltung beim Stoßprozess zweier Kugeln

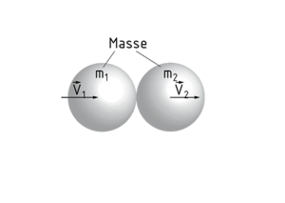
Der Impulserhaltungssatz definiert die Konstanz des Gesamtimpulses in einem abgeschlossenen System.

Bei einem idealen Stoßvorgang ist der Impuls $\overrightarrow{p}$ vor dem Stoß gleich$\overrightarrow{p}'$ nach dem Stoß. Die Wechselwirkung zweier aufeinander stoßender Körper (mit jeweiliger Geschwindigkeit $\overrightarrow{v}$ und Masse m) hat keinen Verlust des Impulses zur Folge.

Es gilt: ${{m}_{1}}{{\overrightarrow{v}}_{1}}+{{m}_{2}}{{\overrightarrow{v}}_{2}}={{m}_{1}}\overrightarrow{v}{{'}_{1}}+{{m}_{2}}\overrightarrow{v}{{'}_{2}}$.

Wechselwirkungen mit der Umgebung, wie zum Beispiel Reibungseffekte, sind ausgeschlossen, da es sich um ein abgeschlossenes System handelt. Dies ist eine theoretische Betrachtungsweise, welche allerdings komplexe Systeme berechenbar machen lässt.

Ein vollkommen abgeschlossenes System zu erzeugen, ist in der Praxis nicht möglich.

动量守恒定律

两个球体碰撞的动量守恒

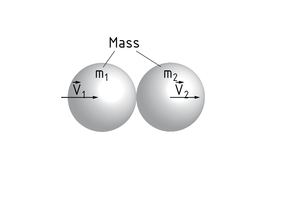
动量守恒定律是指一个封闭系统的总动量保持不变。

在理想的冲击情况下，系统冲击前 $\overrightarrow{p}$ 后 $\overrightarrow{p}'$ 动量不变。两个物体的互相碰撞（以一定的速度 $\overrightarrow{v}$ 和质量m）不会导致总动量的减少。

适用以下公式: ${{m}_{1}}{{\overrightarrow{v}}_{1}}+{{m}_{2}}{{\overrightarrow{v}}_{2}}={{m}_{1}}\overrightarrow{v}{{'}_{1}}+{{m}_{2}}\overrightarrow{v}{{'}_{2}}$ 。

由于名义上系统是封闭的，所以当系统与外界接触时，例如在摩擦力的作用下系统动量将减少。虽然这只是理论研究方法，但它可应用于复杂系统的能量计算中。

实际上，完全封闭的系统是不存在的。

两个球体碰撞的动量守恒

Ley de conservación del impulso

Conservación del impulso durante una colisión entre dos esferas

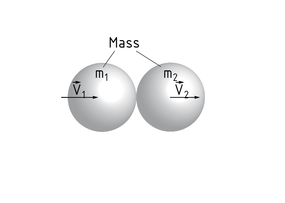
La ley de conservación del impulso define la consistencia del impulso total en un sistema cerrado.En un escenario de impulso ideal, el movimiento $\overrightarrow{p}$ antes del impulso es igual a $\overrightarrow{p}'$ después del impulso. La interacción entre dos cuerpos al colisionar entre sí (con la velocidad $\overrightarrow{v}$ relevante y la masa m) no resulta en una pérdida de impulso.Aplica lo siguiente: ${{m}_{1}}{{\overrightarrow{v}}_{1}}+{{m}_{2}}{{\overrightarrow{v}}_{2}}={{m}_{1}}\overrightarrow{v}{{'}_{1}}+{{m}_{2}}\overrightarrow{v}{{'}_{2}}$.Las interacciones con el ambiente como los efectos de fricción son descontadas, ya que el sistema en cuestión es cerrado. Este es un método teórico, pero posibilita el cálculo de los sistemas complejos. En la práctica, no es posible crear un sistema completamente cerrado.Conservación del impulso durante una colisión entre dos esferas