
Choose one
or multiple languages
0,1,1
- German
- English
- Chinese
- Spanish
Shear stress
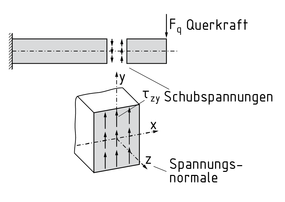
A shear stress$\tau $ is a stress in a sectional area A that is induced by a transverse Force ${{F}_{t}}$ (shear force). It is calculated as follows: $\tau =\frac{{{F}_{q}}}{A}$.
Shear stresses in bodies are generated as a result of Bending, Torsion or the application of transverse forces. There are six different shear stresses in total: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$
The first index position in the shear stress vector (e.g. z in ${{\tau }_{zy}}$) indicates to which stress normal the shear stress belongs (in this case the $\tau =\frac{{{F}_{t}}}{A}$ z-axis), while the second position indicates the direction of the shear stress vector (in this case the y-axis).
In a beam element, shear stresses (e.g. ${{\tau }_{zy}}$) act perpendicular to the beam axis (in this case the z-axis), against the active transverse force ${{F}_{q}}$.
Schubspannung
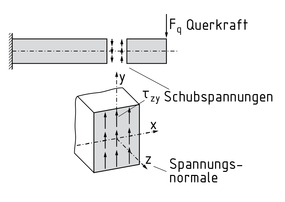
Eine Schubspannung $\tau $ ist eine durch eine Querkraft ${{F}_{q}}$ (Schubkraft) ausgelöste Spannung in einer Schnittfläche A. Sie berechnet sich wie folgt: $\tau =\frac{{{F}_{q}}}{A}$.
In Körpern werden Schubspannungen durch Biegung, Torsion oder durch Aufbringen von Querkräften erzeugt. Insgesamt werden sechs Schubspannungen unterschieden: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$
Die erste Stelle des Indexes des Schubspannungsvektors (z. B. z bei ${{\tau }_{zy}}$) gibt dessen Zugehörigkeit zu der Spannungsnormalen (hier: z-Achse) an, die zweite Stelle die Richtung des Schubspannungsvektors (hier: y-Achse).
In einem Balkenelement wirken Schubspannungen (z. B. ${{\tau }_{zy}}$) quer zu der Balkenachse (hier: z-Achse), entgegen der wirkenden Querkraft ${{F}_{q}}$.
剪应力
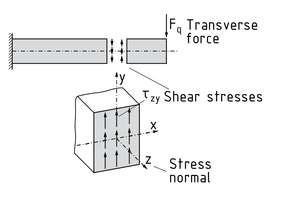
剪应力 $\tau $ 是受到横向力 ${{F}_{t}}$ (或称剪力)的截面 A 内产生的一个应力。其计算方式如下: $\tau =\frac{{{F}_{q}}}{A}$ .
剪应力是由于物体受到弯曲、扭转或横向力而产生的。总共产生 6 个不同的剪应力: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}}$
剪应力矢量的第一个角标字母 (如 ${{\tau }_{zy}}$ 中的 z)指的是垂直于剪应力的应力方向(即此处的 $\tau =\frac{{{F}_{t}}}{A}$ z轴), 第二个角标字母指的是剪应力矢量的方向(即此处的y轴)。
在一个梁单元上,剪应力 (如 ${{\tau }_{zy}}$ )垂直于梁轴线(即此处的z轴),并且与所受的横向力方向相反 ${{F}_{q}}$ 。
作用于梁上的横向力
Esfuerzo de corte
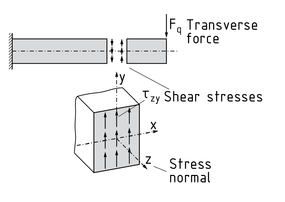
Un esfuerzo de corte $\tau $ es un esfuerzo en un área de sección A que es inducido por una fuerza transversal ${{F}_{t}}$ (fuerza de corte). Se calcula de la siguiente manera: $\tau =\frac{{{F}_{q}}}{A}$ .
Los esfuerzos de corte en los cuerpos son generados como un resultado de la flexión, la torsión o la aplicación de fuerzas transversales. En total, hay seis esfuerzos de corte diferentes: ${{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}} $
La primera posición de índice en el vector de esfuerzo de corte (por ejemplo, z en ${{\tau }_{zy}}$ ) indica a qué normal de esfuerzo pertenece el esfuerzo por corte (en este caso el eje $\tau =\frac{{{F}_{t}}}{A}$ z), mientras que la segunda posición indica la dirección del vector de esfuerzo de corte (en este caso el eje y).
En un elemento de viga, los esfuerzos de corte (por ejemplo, ${{\tau }_{zy}}$ ) actúan perpendiculares al eje de la viga (en este caso el eje z), contra la fuerza transversal activa ${{F}_{q}}$ .
Fuerza transversal en una viga
