Teoría de vigas

Schnittgrößen eines Balkenelements

La teoría de vigas se relaciona con el comportamiento de los elementos oblongos, referidos como vigas, bajo la influencia de fuerzas transversales. El módulo de elasticidad E y el I de la sección de la viga contrarrestan esta carga. Por consiguiente, el comportamiento de una viga depende de las constantes del material y de la geometría de la sección.

La deformación de una viga debido a una fuerza transversal T se llama flexión. La ruta de deformación es referida como línea de flexión.

Asumir la existencia de una y la teoría de vigas de Timoshenko simplifica los cálculos de vigas. En el teorema de Bernoulli, el cual se usa cuando las vigas son muy largas en relación con su altura, las deformaciones por corte son ignoradas. En la teoría de Timoshenko, por otro lado, se las considera. En ambos casos, las secciones permanecen planas por definición. De acuerdo con Timoshenko, una vez que se han sometido a la deformación, las secciones ya no son perpendiculares en relación con el eje de la viga.

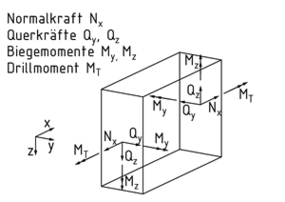
Cada una de las resultantes del esfuerzo de la viga actúa en una dirección en particular en el espacio, lo que significa que hay seis resultantes en cada cara recortada. Las fuerzas transversales ${{T}_{y}}$ y ${{T}_{z}}$ actúan perpendicular al eje de la viga. La fuerza normal ${{N}_{x}}$ actúa en el sentido del eje de la viga. Hay momentos presentes alrededor de las fuerzas relevantes. El momento alrededor del eje de la viga se llama momento de torsión ${{M}_{T}}$ .

Resultante de esfuerzo de un elemento de viga

Balkentheorie

Schnittgrößen eines Balkenelements

Die Balkentheorie beschreibt das Verhalten länglicher Elemente - sogenannter Balken - unter Einfluss von Querkräften. Der Belastung wirken der Elastizitätsmodul E und das Flächenträgheitsmoment I des Balkenquerschnittes entgegen. Somit ist das Verhalten eines Balkens von den Materialkonstanten und der Querschnittsgeometrie abhängig.

Die Verformung, die der Balken durch eine Querkraft Q erfährt, heißt Biegung. Der Verlauf der Verformung wird als Biegelinie bezeichnet.

Vereinfachungen zur Berechnung eines Balkens liefern die Annahme eines Euler-Bernoulli-Balkens und die Timoschenko-Balken-Theorie. In der Theorie von Bernoulli, die bei sehr langen Balken relativ zu ihrer Höhe verwendet wird, werden die Schubverformungen vernachlässigt. Bei Timoschenko werden sie dagegen berücksichtigt. Bei beiden Theorien bleiben die Querschnitte definitionsgemäß eben. Laut Timoschenko stehen die Querschnitte nach der Verformung nicht mehr senkrecht zur Balkenachse.

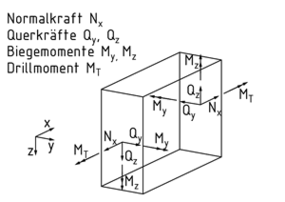
Die Schnittgrößen eines Balkens sind jeweils in eine Raumrichtung orientiert, sodass sechs Größen pro Schnittufer vorhanden sind. Es wirken die Querkräfte${{Q}_{y}}$ und ${{Q}_{z}}$ senkrecht zur Balkenachse. In Richtung der Balkenachse wirkt die Normalkraft ${{N}_{x}}$. Um die jeweiligen Kräfte sind Momente vorhanden. Das Moment um die Balkenachse wird als Drillmoment ${{M}_{T}}$bezeichnet.

Beam theory

Stress resultants of a beam element

The beam theory relates to the behaviour of oblong elements - referred to as beams - under the influence of transverse forces. The Modulus of elasticity E and the Area moment of inertia I of the beam cross-section counteract this load. Consequently, a beam's behaviour depends on the Material constants and the cross-sectional geometry.

A beam's deformation due to a transverse Force T is called Bending. The deformation path is referred to as the bending line.

The assumption of an Euler-Bernoulli beam and the Timoshenko beam theory simplify beam calculations. In Bernoulli's theorem, which is used when beams are very long in relation to their height, the shear deformations are ignored. In the Timoshenko theory, on the other hand, they are taken into account. In both cases, the cross-sections remain planar by definition. According to Timoshenko, once they have been subject to deformation, the cross-sections are no longer perpendicular to the beam axis.

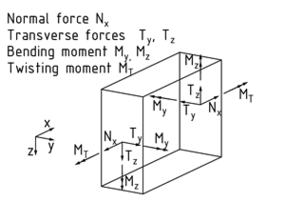
Each of a beam's Stress resultants acts in a particular direction in space, which means there are six resultants for each cut face. The transverse forces${{T}_{y}}$ and ${{T}_{z}}$ act perpendicular to the beam axis. The normal force ${{N}_{x}}$ acts in the direction of the beam axis. Moments are present around the relevant forces. The moment around the beam axis is called the twisting moment ${{M}_{T}}$.

梁理论

一个梁单元的内应力

梁理论 指在横向力作用下长方形单元梁的行为变化。 杨氏模量 E 和在梁在节面处的 I抵消此载荷。 因此， 材料常数和横截面几何结构决定了横梁的行为变化。

由于横向力作用导致梁发生变形的过程 T 称为折弯。折弯路径称为 折弯线。

和 铁木辛柯梁理论 的假设可以简化梁的计算。 在伯努利定理中（适用于长度远大于宽度的梁），剪切变形可以忽略不计。 然而在铁木辛柯梁理论中则考虑了剪切变形。 在这两个理论中，横截面保持为平面。 根据铁木辛柯梁理论， 当梁发生变形时，横截面则不再垂直于梁的轴向方向。

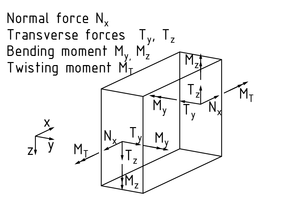
每一个梁的内应力在空间中均有特定的方向，意味着在每个截面存在6种内应力。 横向力 ${{T}_{y}}$ 和 ${{T}_{z}}$ 垂直于梁的轴线。 法向力 ${{N}_{x}}$ 沿着梁的轴线方向。 力矩伴随着力存在。在梁轴线上的力矩称为转矩 ${{M}_{T}}$ 。

一个梁单元的内应力