
Seleccione uno
o más idiomas
0,1,3
- Alemán
- Inglés
- Chino
- Español
Principio de D'Alembert
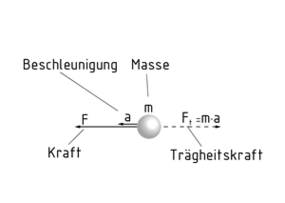
El principio de D'Alembert se usa para calcular un sistema dinámico desde un punto de vista estático. El introducir una fuerza de inercia ${{F}_{\tau }}$ (fuerza auxiliar de D?Alembert) como una fuerza ficticia, se crea un equilibrio en el sistema, ya que la suma de las fuerzas externas ${{F}_{R}}$ corresponde a la fuerza de inercia ${{F}_{\tau }}$ .
La fuerza de inercia es causada por la masa m del sistema dinámico y por lo tanto actúa en su centro de gravedad. La fuerza de inercia actúa en la dirección opuesta a la aceleración a y, por lo tanto, a la del movimiento del sistema. Es el producto de la masa m y la aceleración a. Como se asume que el sistema a ser calculado se mueve en dirección positiva, la fuerza de inercia es precedida por un signo negativo. Aplica lo siguiente: ${{F}_{\tau }}=-m\cdot a$
Fuerza auxiliar de d'Alembert en un cuerpo en movimiento
D'Alembertsches Prinzip
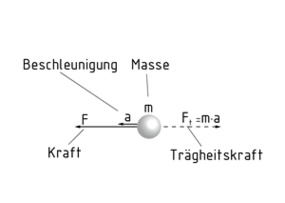
Das Prinzip von d'Alembert ermöglicht die Berechnung eines dynamischen Systems unter statischer Betrachtungsweise. Die Einführung der d'Alembertschen Trägheitskraft ${{F}_{\tau }}$ als eine sogenannte Scheinkraft bringt das System in ein Gleichgewicht, da die Summe der äußeren Kräfte ${{F}_{R}}$ betragsmäßig der Trägheitskraft ${{F}_{\tau }}$ entspricht.
Die Trägheitskraft wird durch die Masse m des bewegten Systems verursacht und greift deshalb in dessen Schwerpunkt an. Entgegengesetzt der Beschleunigung a und somit entgegengesetzt der Richtung der Bewegung des Systems, ist die Trägheitskraft gerichtet. Sie ist das Produkt aus Masse m und Beschleunigung a. Da die Bewegungsrichtung des zu berechnenden Systems als positiv angenommen wird, hat die Trägheitskraft ein negatives Vorzeichen. Es gilt: ${{F}_{\tau }}=-m\cdot a$
D'Alembert's principle
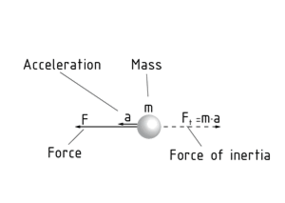
The principle of d'Alembert is used to calculate a dynamic system from a static perspective. Introducing a Force of inertia ${{F}_{\tau }}$ (d'Alembert's auxiliary force) as a fictitious force creates an Equilibrium in the system, because the sum of the external forces ${{F}_{R}}$ corresponds to the force of inertia ${{F}_{\tau }}$.
The force of inertia is caused by the mass m of the dynamic system and therefore acts at its Centre of gravity. The force of inertia acts in the opposite direction to the acceleration a and thus to the system's motion. It is the product of mass m and acceleration a. Since the system to be calculated is assumed to be moving in a positive direction, the force of inertia is preceded by a negative sign. The following applies: ${{F}_{\tau }}=-m\cdot a$
达朗贝尔原理
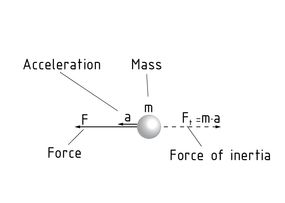
达朗贝尔原理是指采用静态的方法来计算动态系统的问题。由于物体的合外力${{F}_{R}}$与惯性力${{F}_{\tau }}$相对应,所以引用虚构的惯性力 ${{F}_{\tau }}$ (达朗贝尔辅助力)可以建立系统的平衡。
由动态系统的质量m引起的力称为惯性力,它作用在系统的重心位置。惯性力的作用方向与物体加速度a和运动方向相反,它可由质量m与加速度值a计算得到。假设目标系统沿正方向行进,那么在计算惯性力的等式前应添加负号。应用如下: ${{F}_{\tau }}=-m\cdot a$
运动物体的达朗贝尔辅助力
