
Seleccione uno
o más idiomas
0,1,3
- Alemán
- Inglés
- Chino
- Español
Determinación estática
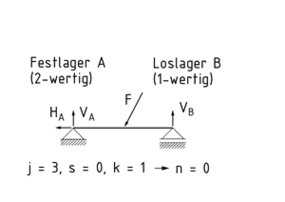
Se dice que un sistema estático presenta una determinación estática cuando tiene el mismo número de grados de libertad que de reacciones de soporte. Las reacciones de soporte pueden calcularse sobre la base de las condiciones de equilibrio de las cargas externas.
Existen seis condiciones de equilibrio en un espacio tridimensional. Las primeras tres describen la suma total de todas las fuerzas en las tres dimensiones (x, y, z). Las otras tres ecuaciones describen la suma total de los momentos alrededor de los tres ejes espaciales. Todas las ecuaciones dan como resultado cero.
El grado n de indeterminación estática se calcula del siguiente modo:
$n=j+s-6k$ (tridimensional) o $n=j+s-3k$ (bidimensional)
j es la suma total de todas las reacciones de los soportes (valencia), s es la suma total de todas las reacciones de las conexiones (valencia), y k es el número de cuerpos a ser modelados en un diagrama de cuerpo libre.
Si consideramos una armadura con un número z de uniones, s miembros y a fuerzas de soporte, el grado de indeterminación se calcula del siguiente modo: $n=a+s-2s$
Si n = 0, la armadura presenta determinación estática.
Un sistema estáticamente determinado
Statische Bestimmtheit
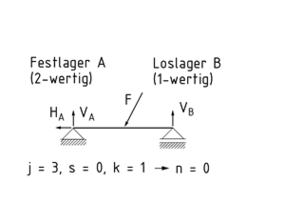
Die statische Bestimmtheit eines statischen Systems ist bei der gleichen Anzahl von Freiheitsgraden wie Lagerreaktionen gegeben. Aus den Gleichgewichtsbedingungen der äußeren Belastungen sind dann die Lagerreaktionen errechenbar.
Im dreidimensionalen Raum gelten sechs Gleichgewichtsbedingungen. Die ersten drei beschreiben die Summe aller Kräfte in die Raumrichtung (x, y, z). Die weiteren drei Gleichungen beschreiben die Summe der Momente um die drei Raumachsen. Alle Gleichungen ergeben null.
Der Grad n der statischen Unbestimmtheit errechnet sich durch:
$n=j+s-6k$ (dreidimensional) bzw. $n=j+s-3k$ (zweidimensional)
Das j ist gleich der Summe aller Wertigkeiten der Lager, s entspricht der Summe aller Wertigkeiten der Verbindungen und k ist die Anzahl der freizuschneidenden Körper.
Liegt ein Fachwerk mit einer Anzahl von z Gelenken, s Stäben und a Auflagereaktionen vor, so lässt sich der Grad der Unbestimmtheit wie folgt berechnen: $n=a+s-2s$
Bei n = 0 liegt ein statisch bestimmtes System vor.
Static determinacy
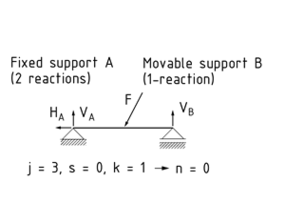
A static system is said to exhibit static determinacy when it has the same number of degrees of freedom as support reactions. The support reactions can be calculated based on the conditions of Equilibrium of the external loads.
There are six conditions of equilibrium in a three-dimensional space. The first three describe the sum total of all forces in all three dimensions (x, y, z). The other three equations describe the sum total of moments around the three spatial axes. All the equations result in zero.
The degree n of static indeterminacy is calculated as follows:
$n=j+s-6k$ (three-dimensional) and/or $n=j+s-3k$ (two-dimensional)
j is the sum total of all the reactions from the supports (valency), s is the sum total of all the reactions from the connections (valency) and k is the number of bodies to be modelled in a free body diagram.
If we consider a Truss with a number z of joints, s members and a supporting forces, the degree of indeterminacy is calculated thus: $n=a+s-2s$
If n = 0, the truss exhibits static determinacy.
静定性
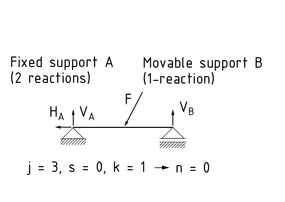
当一个静态系统与其支撑反力具有相同的自由度时,该系统具有静定性。支撑反力可由外部载荷的平衡条件计算得到。
在三维空间中,系统有 6 个平衡条件。前3个条件描述了 x, y, z 三个方向力的总和。其他 3个平衡条件描述了绕着三个空间轴力矩的总和。所有的等式和为 0。
静不定程度n可由以下公式计算:
$n=j+s-6k$ (三维) 且/或 $n=j+s-3k$ (二维)
j指所有支撑反力(价)的总和,s指所有连接处反力(价)的总和,k指受力图中物体的数量。
如果假设一个桁架有 z 个节点, s 个杆件和a个支持力,其静不定程度可由公式 $n=a+s-2s$ 计算得到。
如果 n=0 ,此桁架具有静定性。
一个静定系统
