Tensor de deformación

Scherung eines Quaders

El tensor de deformación $\varepsilon $ indica el estado de deformación del cuerpo y, por lo tanto, su elongación ( ${{\varepsilon }_{x}}$ , ${{\varepsilon }_{y}}$ , ${{\varepsilon }_{z}}$ ) y corte $({{\gamma }_{xy}}={{\gamma }_{yx}},{{\gamma }_{xz}}={{\gamma }_{zx}},{{\gamma }_{yz}}={{\gamma }_{yz}})$ . Todos los componentes se combinan en una matriz y forman el tensor de deformación $\varepsilon $:

$\varepsilon =\left( \begin{matrix} {{\varepsilon }_{x}} & \frac{1}{2}{{\gamma }_{xy}} & \frac{1}{2}{{\gamma }_{xz}} \\ \frac{1}{2}{{\gamma }_{xy}} & {{\varepsilon }_{y}} & \frac{1}{2}{{\gamma }_{yz}} \\ \frac{1}{2}{{\gamma }_{xz}} & \frac{1}{2}{{\gamma }_{yz}} & {{\varepsilon }_{z}} \\\end{matrix} \right)$

La elongación $\varepsilon $ indica el cambio en la longitud en relación con la longitud total del cuerpo. Este índice corresponde al eje de elongación.

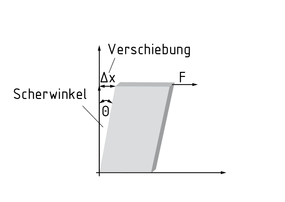
El corte $\gamma $ de un paralelepípedo rectangular bajo una fuerza F toma la forma de un desplazamiento relativo $\Delta x$ en los lados. Los bordes del paralelepípedo rectangular son desplazados en un ángulo de $\Theta $ . El plano en el cual ha sido desplazado el borde se indica en el índice del componente de corte relevante.

El corte ${{\gamma }_{xy}}$ , por ejemplo, indica un cambio de ángulo en el plano x-y.

Corte de un paralelepípedo rectangular

Verzerrungstensor

Scherung eines Quaders

Der Verzerrungstensor$\varepsilon $ beschreibt den Verzerrungszustand und somit die vorhandene Dehnung (${{\varepsilon }_{x}}$, ${{\varepsilon }_{y}}$, ${{\varepsilon }_{z}}$) sowie Gleitung bzw. Scherung $({{\gamma }_{xy}}={{\gamma }_{yx}},{{\gamma }_{xz}}={{\gamma }_{zx}},{{\gamma }_{yz}}={{\gamma }_{yz}})$ eines Körpers. Alle Komponenten werden in einer Matrix zusammengefasst und bilden den Verzerrungstensor $\varepsilon $:

$\varepsilon =\left( \begin{matrix}{{\varepsilon }_{x}} & \frac{1}{2}{{\gamma }_{xy}} & \frac{1}{2}{{\gamma }_{xz}} \\\frac{1}{2}{{\gamma }_{xy}} & {{\varepsilon }_{y}} & \frac{1}{2}{{\gamma }_{yz}} \\\frac{1}{2}{{\gamma }_{xz}} & \frac{1}{2}{{\gamma }_{yz}} & {{\varepsilon }_{z}} \\\end{matrix} \right)$

Die Dehnung $\varepsilon $ gibt die Längenänderung relativ zur Gesamtlänge eines Körpers an. Ihr Index entspricht der Koordinatenachse, in der sie stattfindet.

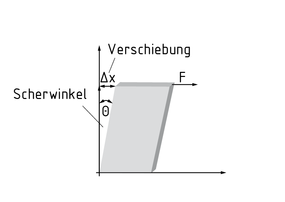
Die Scherung $\gamma$ eines Quaders, die unter einer Kraft F ausgelöst wird, bedeutet eine Verschiebung$\Delta x$ der Seitenflächen zueinander. Die Kanten des Quaders verschieben sich dabei unter einem Winkel $\Theta $. Die Ebene, in welcher sich die Kante verschoben hat, ist im Index der jeweiligen Komponente der Gleitung zu finden.

Die Gleitung ${{\gamma }_{xy}}$beschreibt z. B. eine Winkeländerung in der x-y-Ebene.

Strain tensor

Shear of a rectangular parallelepiped

The strain tensor$\varepsilon $ indicates a body's state of strain and thus its elongation (${{\varepsilon }_{x}}$, ${{\varepsilon }_{y}}$, ${{\varepsilon }_{z}}$) and shear $({{\gamma }_{xy}}={{\gamma }_{yx}},{{\gamma }_{xz}}={{\gamma }_{zx}},{{\gamma }_{yz}}={{\gamma }_{yz}})$. All components are combined in a Matrix and form the strain tensor $\varepsilon $:

$\varepsilon =\left( \begin{matrix}{{\varepsilon }_{x}} & \frac{1}{2}{{\gamma }_{xy}} & \frac{1}{2}{{\gamma }_{xz}} \\\frac{1}{2}{{\gamma }_{xy}} & {{\varepsilon }_{y}} & \frac{1}{2}{{\gamma }_{yz}} \\\frac{1}{2}{{\gamma }_{xz}} & \frac{1}{2}{{\gamma }_{yz}} & {{\varepsilon }_{z}} \\\end{matrix} \right)$

The elongation $\varepsilon $ indicates the change in length in relation to a body's total length. Its index corresponds to the axis of elongation.

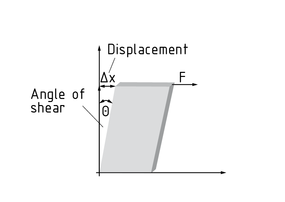
A rectangular parallelepiped's shear $\gamma$ under a Force F takes the form of a relative displacement $\Delta x$ of the sides. The rectangular parallelepiped's edges are displaced at an angle $\Theta $. The plane in which the edge has been displaced is indicated in the index of the relevant shear component.

The shear ${{\gamma }_{xy}}$, for example, indicates a change of angle in the x-y plane.

应变张量

长方体的角应变

应变张量 $\varepsilon $ 是指物体的应变状态及其线应变 ( ${{\varepsilon }_{x}}$ , ${{\varepsilon }_{y}}$ , ${{\varepsilon }_{z}}$ ) 和 角应变 $({{\gamma }_{xy}}={{\gamma }_{yx}},{{\gamma }_{xz}}={{\gamma }_{zx}},{{\gamma }_{yz}}={{\gamma }_{yz}})$ 。所有上述元素形成了应变张量 $\varepsilon $，用矩阵表示为：

$\varepsilon =\left( \begin{matrix} {{\varepsilon }_{x}} & \frac{1}{2}{{\gamma }_{xy}} & \frac{1}{2}{{\gamma }_{xz}} \\ \frac{1}{2}{{\gamma }_{xy}} & {{\varepsilon }_{y}} & \frac{1}{2}{{\gamma }_{yz}} \\ \frac{1}{2}{{\gamma }_{xz}} & \frac{1}{2}{{\gamma }_{yz}} & {{\varepsilon }_{z}} \\\end{matrix} \right)$

线应变 $\varepsilon $ 是指物体的长度增量与物体总长的比值。其角标对应于发生线应变的轴。

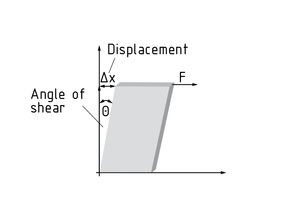
长方体受到作用力F产生角应变 $\gamma $，与 x 轴产生相对位移 $\Delta x $ 。长方体的侧边产生应变角 $\Theta $ 。其角标表示为长方体位移所在的平面。

如角应变 ${{\gamma }_{xy}}$ 是指 x-y 平面内角度的改变量。

长方体的角应变