
Seleccione uno
o más idiomas
0,1,3
- Alemán
- Inglés
- Chino
- Español
Oscilador torsional
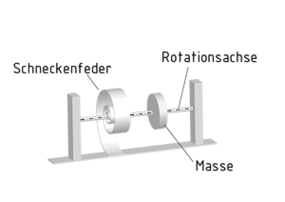
Un oscilador torsional consiste en una masa en rotación m, la cual, debido al efecto de un resorte en voluta o barra de torsión, por ejemplo, se somete a un momento de restauración $\overrightarrow{M}$alrededor del eje de rotación.
El momento de restauración $\overrightarrow{M}$ es proporcional y actúa en dirección opuesta al ángulo de una desviación $\overrightarrow{\varphi }$. Con el momento director D, aplica lo siguiente: $\overrightarrow{M}=-D\cdot \overrightarrow{\varphi }$ . El momento director D es comparable con la constante de resorte c en un sistema de resorte-masa. Sin embargo, la unidad es diferente, porque el movimiento es rotativo.
La frecuencia angular natural $\omega $ de un oscilador torsional se calcula de la siguiente manera: $\omega =\sqrt{\frac{D}{J}}$ .
El momento de inercia J de la masa aparece en la misma posición en la fórmula que la masa m en la fórmula del sistema de resorte-masa.
El tiempo periódico ${{T}_{0}}$ del oscilador torsional es la frecuencia angular natural $\omega $ multiplicada por $2\pi $ .
Oscilador torsional
Drehschwinger
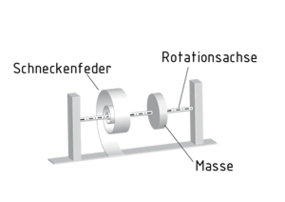
Ein Drehschwinger besteht aus einer drehbar gelagerten Masse m, die z. B. durch eine Schneckenfeder oder einen Torsionsstab ein rückstellendes Moment $\overrightarrow{M}$um die Rotationsachse erfährt.
Das rückstellende Moment $\overrightarrow{M}$ verhält sich proportional und ist entgegengesetzt zum Winkel einer Auslenkung $\overrightarrow{\varphi }$ gerichtet. Mit dem Direktionsmoment D gilt $\overrightarrow{M}=-D\cdot \overrightarrow{\varphi }$. Das Direktionsmoment D ist vergleichbar mit der Federkonstante c in einem Federmassesystem. Es hat jedoch eine andere Einheit, da es sich hier um eine rotatorische Bewegung handelt.
Für die Eigenkreisfrequenz $\omega $ eines Drehschwingers gilt: $\omega =\sqrt{\frac{D}{J}}$.
Im Quotient der Formel ist das Massenträgheitsmoment J - anders als beim Federmassesystem, bei dem dort die Masse m steht.
Die Periodendauer ${{T}_{0}}$ des Drehschwingers ergibt sich aus dem Produkt der Eigenkreisfrequenz $\omega $ und $2\pi $.
Torsional oscillator
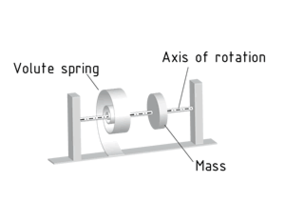
A torsional oscillator consists of a rotating mass m, which - due to the effect of a volute spring or Torsion bar, for example - is subject to a restoring moment $\overrightarrow{M}$about the axis of Rotation.
The restoring moment $\overrightarrow{M}$ is proportional and acts in the opposite direction to the angle of a deflection $\overrightarrow{\varphi }$. With the directing moment D, the following applies: $\overrightarrow{M}=-D\cdot \overrightarrow{\varphi }$. The directing moment D is comparable to the spring constant c in a Spring-mass system. The unit is different, though, because the motion is rotational.
A torsional oscillator's natural Angular frequency $\omega $ is calculated as follows: $\omega =\sqrt{\frac{D}{J}}$.
The mass moment of inertia J appears in the same position in the formula as the mass m in the spring-mass system formula.
The torsional oscillator's periodic time ${{T}_{0}}$ is the natural angular frequency $\omega $ multiplied by $2\pi $.
扭转振荡器
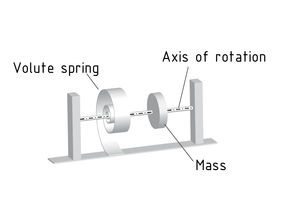
扭转振荡器 包含由涡簧或扭杆作用产生的旋转块m,在旋转轴方向承受一个回复力矩 $\overrightarrow{M}$。
回复力矩 $\overrightarrow{M}$ 与变形成正比例,并且作用方向与挠角方向 $\overrightarrow{\varphi }$ 相反。当轴向力矩为D时,遵从下列公式: $\overrightarrow{M}=-D\cdot \overrightarrow{\varphi }$ 。 轴向力矩D相当于弹簧-质量系统中的弹簧常数c。 然而两者的单位不同,这是由于这里的运动是扭转。
扭转振荡器的固有角频率 $\omega $ 可用下列公式计算: $\omega =\sqrt{\frac{D}{J}}$ 。
质量惯性矩 J 在公式中的位置与弹簧-质量系统中m 位置相同。
扭转振荡器的 周期 ${{T}_{0}}$ 等于 固有角频率 $\omega $ 乘以 $2\pi $ 。
扭转振荡器
